Trabalhando com Material Dourado e Blocos Lógicos nas Séries Iniciais (página 2)

Embora esse material permitisse que as próprias crianças compusessem as dezenas e centenas, a imprecisão das medidas dos quadrados e cubos constituía um problema ao serem realizadas atividades com números decimais e raiz quadrada, entre outras aplicações possíveis para o material de contas. Foi por isso que Lubienska de Lenval, seguidor de Montessori, fez uma modificação no material inicial e o construiu em madeira, na forma que encontramos atualmente.

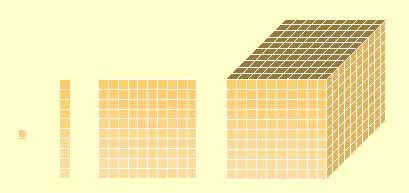
O nome "Material Dourado" vem do original "Material de Contas Douradas". Em analogia às contas, o material apresenta sulcos em forma de quadrados. Pode-se fazer uma adaptação do material dourado para o trabalho em sala de aula, com papel quadriculado de 1cm X 1 cm, onde as peças são feitas da seguinte forma:

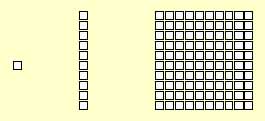
unidade           dezena           centena

 (1 X1)           (1 X 10)         (10 X 10)

O material em papel possui a limitação de impossibilitar a construção do bloco, o que é uma desvantagem em relação ao material em madeira.

O primeiro contato do aluno com o material deve ocorrer de forma lúdica, para que ele possa explorá-lo livremente. É nesse momento que a criança percebe a forma, a constituição e os tipos de peça do material.

Ao desenvolver as atividades, o professor pode pedir às crianças que elas mesmas atribuam nomes aos diferentes tipos de peças do material, criando uma forma própria de registrar o que vão fazendo. Seria conveniente que o professor trabalhasse durante algum tempo com a linguagem das crianças, para depois adotar os nomes convencionais: cubinho, barra, placa e bloco.

O material dourado destina-se a atividades que auxiliem o ensino e a aprendizagem do sistema de numeração decimal-posicional e dos métodos para efetuar as operações fundamentais (ou seja, os algoritmos). No ensino tradicional, as crianças acabam "dominando" os algoritmos a partir de treinos cansativos, sem conseguirem compreender o que fazem. Com o material dourado, a situação é outra: as relações numéricas abstratas passam a ter uma imagem concreta, facilitando a compreensão. Obtém-se, então, além da compreensão dos algoritmos, um notável desenvolvimento do raciocínio e um aprendizado bem mais agradável.

O material, mesmo sendo destinado ao trabalho com números (na matemática), pode ser utilizado com crianças de até seis anos de idade, para desenvolver a criatividade, motricidade e o raciocínio lógico-matemático.

ATIVIDADES:

1. JOGOS LIVRES

Objetivo: tomar contato com o material de maneira livre, sem regras.

Durante algum tempo, os alunos brincam com o material, fazendo construções livres. O material dourado é construído de maneira a representar um sistema de agrupamento. Sendo assim, muitas vezes as crianças descobrem sozinhas relações entre as peças. Por exemplo, podemos encontrar alunos que concluem:
- Ah! A barra é formada por 10 cubinhos!
- E a placa é formada por 10 barras!
- Veja, o cubo é formado por 10 placas!

2. MONTAGEM

Objetivo: perceber as relações que há entre as peças.

O professor sugere as seguintes montagens:
- uma barra;
- uma placa feita de barras;
- uma placa feita de cubinhos;
- um bloco feito de barras;
- um bloco feito de placas;

O professor estimula os alunos a obterem conclusões com perguntas como estas:
- Quantos cubinhos vão formar uma barra?
- E quantos formarão uma placa?
- Quantas barras preciso para formar uma placa?

Nesta atividade, também é possível explorar conceitos geométricos, propondo desafios como estes:
- Vamos ver quem consegue montar um cubo com 8 cubinhos? É possível?
- E com 27? É possível?

Voltar para a primeira página deste artigo